3. Variant calling and genotype likelihood

Learning outcome

After this chapter, the students can describe the pipeline used for variant calling with the GATK package. They can browse the intermediate data files and explain the relationships between different features within them. They can describe the approach used for determining the genotype of a sample at a specific genome position and compute the likelihoods of alternative genotypes given the observed bases.

Varian calling of many samples

Our workflow for variant calling is the following:

flowchart LR
    subgraph sample_1
    style sample_1 fill:#fdf2e9
    fastq_1["&emsp13;fastq_1&ensp;"] --> bam_1["&emsp13;bam_1&ensp;"]
    bam_1 --> gvcf_1["&emsp13;gvcf_1&ensp;"]
    end
    subgraph sample_2
    style sample_2 fill:#fdf2e9
    fastq_2["&emsp13;fastq_2&ensp;"] --> bam_2["&emsp13;bam_2&ensp;"]
    bam_2 --> gvcf_2["&emsp13;gvcf_2&ensp;"]
    end
    subgraph sample_n
    style sample_n fill:#fdf2e9
    fastq_n["&emsp13;fastq_n&ensp;"] --> bam_n["&emsp13;bam_n&ensp;"]
    bam_n --> gvcf_n["&emsp13;gvcf_n&ensp;"]
    end
    subgraph sample_100
    style sample_100 fill:#fdf2e9
    fastq_100 --> bam_100
    bam_100 --> gvcf_100
    end

    gvcf_1 --> gvcf
    gvcf_2 --> gvcf
    gvcf_n --> gvcf
    gvcf_100 --> gvcf

    subgraph all_samples
    style all_samples fill:#fdf2e9
    gvcf --> vcf
    end

This roughly follows the GATK Best Practices Guideline for Germline short variant discovery.

Our target is one the extreme right, a VCF file holding the variant information of all (in our case, 100) samples. we see that the task can be split such that each sample is processed independently until the GVCF state; these are then combined into one large GVCF file and “joint-called” to create a VCF file. The data files processed in real studies can be massive- In our case, the data represent a fraction of the genome but the files are still fairly large. The two FASTQ files for one sample (‘fastq_1’) are 32 MB each and the BAM file (‘bam_1’) is 62 MB. This is reduced to 24 MB as GVCF (‘gvcf_1’), but the combined GVCF (‘gvcf’) is then 2.5 GB. The final VCF (‘vcf’) is 194 MB in size. What explains that?

VCF – the Variant Call Format

The VCF format is specified at https://samtools.github.io/hts-specs/VCFv4.2.pdf. In principle, the VCF files are huge tables that start with a (possibly massive) header:

The header explains what is in the table below (RECORDS) and, for example, keeps track of the program commands and their parameters that were used to create the VCF file.

The RECORDS part differs from what we have used to seeing for biological sequences. A classical alignment of protein sequences may look like this:

Sequences of different individuals are horizontally on own roads and the column indicate inferred homologous positions. A small alignment for the samples S1-S4 could look like this:

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
S1	C	C	G	T	C	A	C	A	C	T	A	A	C	A	G	C	T	A	C	C
S2	C	C	G	T	C	A	C	A	C	T	A	A	C	A	G	C	T	G	C	C
S3	C	C	G	T	C	A	C	A	T	T	A	A	C	A	G	C	T	G	C	C
S4	C	C	G	T	C	A	C	A	C	T	A	A	C	A	G	C	T	G	C	C

The challenge is that, in genomic analyses, the sequences can be very long and the number of columns would be several orders of magnitude greater than the number of rows. Instead of having the sequence positions horizontally, VCF files have them vertically:

	S1	S2	S3	S4
1	C	C	C	C
2	C	C	C	C
3	G	G	G	G
4	T	T	T	T
5	C	C	C	C
6	A	A	A	A
7	C	C	C	C
8	A	A	A	A
9	C	C	T	C
10	T	T	T	T
11	A	A	A	A
12	A	A	A	A
13	C	C	C	C
14	A	A	A	A
15	G	G	G	G
16	C	C	C	C
17	T	T	T	T
18	A	G	G	G
19	C	C	C	C
20	C	C	C	C

Next we notice that the table is massively redundant as the same nucleotide is present in all samples. We could simplify it by specifying the reference sequence separately and then only reporting the positions where the samples differ from that:

Reference:
>CHR1 CGTCACACTAACAGCTGCCCATCTGGTTACTGTCAGGGAGAAAACAACTGAGCTTGCGGA

	S1	S2	S3	S4
9	C	C	T	C
18	A	G	G	G

We are getting very close to a VCF file. The true VCF RECORDS section is approximately like this (in reality, there’s lot’s of additional information):

CHROM	POS	REF	ALT	S1	S2	S3	S4
CHR1	9	C	T	0	0	1	0
CHR1	18	G	A	1	0	0	0

Here, the first two columns tell the sequence name and position in that, and the next two column the reference allele (as observed in the reference sequence) and the alternative character(s). The four last columns tell the genotypes of the samples S1-S4, i.e. which allele the samples have. In that, 0 refer to the REF allele and 1 (and greater numbers) to the ALT allele(s).

This VCF would be valid for a haploid sequence such as the mitochondrion or the human Y chromosome. For a diploid sequence, the genotypes would tell the two alleles the individual has, in this case either “0/0”, “0/1” or “1/1” for homozygote REF, heterozygote and homozygote ALT, respectively. In some cases the genotype alleles are separated by a bar “|” and not by a slash “/”: this tells that the data are phased such that the alleles inherited from the mother and the father are arranged consistently at different positions. There is a common practice that unphased heterozygotes are always marked as “0/1”; phased ones can be “0|1” or “1|0”. (In our data only nearby variants may be phased. If they appear in the same read, they must come from the same parent.) Missing data is indicated with dots, e.g. as “./.” for a diploid sequence.

Given that, this small dataset could be represented as a VCF file:

##fileformat=VCFv4.2
##contig=<ID=CHR1,length=20>
#CHROM  POS ID  REF ALT QUAL    FILTER  INFO    FORMAT  S1  S2  S3  S4
CHR1    9   .   C   T   .   .   .   GT  0   0   1   0
CHR1    18  .   G   A   .   .   .   GT  1   0   0   0

The columns are not aligned and it may be difficult for humans to read. However, it can be compressed and indexed, and it then works as a real VCF file:

$ bcftools view chr1.vcf.gz CHR1:9

##fileformat=VCFv4.2
##FILTER=<ID=PASS,Description="All filters passed">
##contig=<ID=CHR1,length=20>
##bcftools_viewVersion=1.18+htslib-1.18
##bcftools_viewCommand=view chr1.vcf.gz CHR1:9; Date=Fri Oct  4 13:46:57 2024
#CHROM  POS ID  REF ALT QUAL    FILTER  INFO    FORMAT  S1  S2  S3  S4
CHR1    9   .   C   T   .   .   .   .   .   .   .   .

Note that the outputted VCF file differs from the original as only one position was selected and the command used for that is tracked.

GVCF vs. VCF

DNA sequencing never produces an uniform coverage across all the genome positions. We saw earlier that with the moderate sequencing depth used in population genetic studies, the chances are high that some positions contain no reads at all. These positions are then considered as “missing data”. It crucial to take that into account in short-read data analyses.

Let’s assume that we have incomplete data like this:

	S1	S2	S3	S4
1	C	C	C	C
2	.	C	C	C
3	.	G	G	G
4	T	T	T	T
5	C	C	C	C
6	A	A	A	A
7	C	C	C	.
8	A	A	A	.
9	C	C	T	.
10	T	T	T	.
11	A	A	A	A
12	A	.	A	A
13	C	.	C	C
14	A	.	A	A
15	G	G	G	G
16	C	C	C	C
17	T	T	.	T
18	A	G	.	G
19	C	C	.	C
20	C	C	.	C

However, our analysis pipeline starts like this:

flowchart LR
    subgraph sample_n
    direction LR
    style sample_n fill:#fdf2e9
    fastq_n["&emsp13;fastq_n&ensp;"] --> bam_n["&emsp13;bam_n&ensp;"]
    bam_n --> gvcf_n["&emsp13;gvcf_n&ensp;"]
    end

    subgraph sample_1
    direction LR
    style sample_1 fill:#fdf2e9
    fastq_1["&emsp13;fastq_1&ensp;"] --> bam_1["&emsp13;bam_1&ensp;"]
    bam_1 --> gvcf_1["&emsp13;gvcf_1&ensp;"]
    end

that is, every sample is processed individually.

If we would analyse the samples separately, we would get this for S1

CHROM	POS	REF	ALT	S1
CHR1	18	G	A	1

and this for S3:

CHROM	POS	REF	ALT	S3
CHR1	9	C	T	1

while S2 and S4 would not have any variants. When combined, we would have this “VCF”:

CHROM	POS	REF	ALT	S1	S2	S3	S4
CHR1	9	C	T	0	0	1	0
CHR1	18	G	A	1	0	0	0

It looks correct but how can we be sure that S4 doesn’t have a variant in position 9 if we don’t have any data? It was marked missing above. Or S3 in position 18? Or any other samples where they don’t have data.

At the minimum, we should be able to correct our data to look like this:

CHROM	POS	REF	ALT	S1	S2	S3	S4
CHR1	9	C	T	0	0	1	.
CHR1	18	G	A	1	0	.	0

Now, the samples with missing data are marked as unknown (“.”) at the positions where other samples are known to vary.

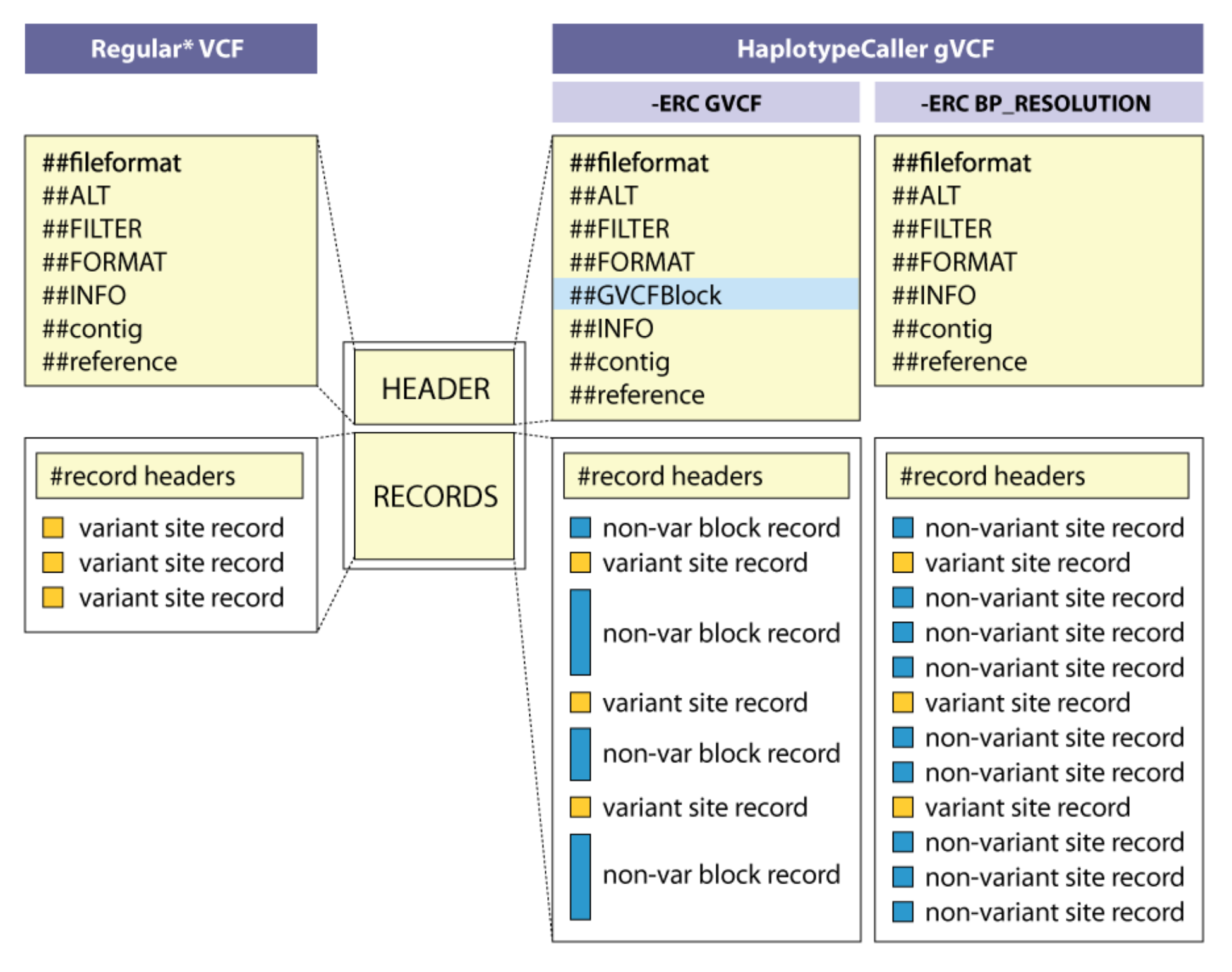
The trick to integrate the information about missing data is not to call the individual samples as plain VCF but as GVCF, standing for Genomic Variant Call format. The concept is explained at the GATK website and in the figure below:

The simplest approach is to record for every site how certain we are that this individual does not contain variant at that position (“-ERC BP_RESOLUTION”, on the extreme right). The downside is that every site will be recorded, making the GVCF RECORDS part over three billion lines long for a human sample. For a sample studied on this course, the beginning of the RECORDS part looks like this:

ctg7180000005484  1   .  C  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  2   .  G  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  3   .  T  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  4   .  C  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  5   .  A  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  6   .  C  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  7   .  A  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  8   .  C  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  9   .  T  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  10  .  A  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  11  .  A  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  12  .  C  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  13  .  A  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  14  .  G  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  15  .  C  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  16  .  T  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  17  .  G  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  18  .  C  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  19  .  C  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0
ctg7180000005484  20  .  C  <NON_REF>  .  .  .  GT:AD:DP:GQ:PL  0/0:0,0:0:0:0,0,0

A more space-efficient approach is to divide the non-variant regions into blocks with approximately equal certainty of non-variant (“-ERC GVCF”, in the middle).

For the same sample, the first line of the RECORDS part looks like this:

ctg7180000005484  1      .  C  <NON_REF>  .  .  END=11503  GT:DP:GQ:MIN_DP:PL  0/0:0:0:0:0,0,0

It says that from position 1 to 11503, the certainty of non-variant is zero.

The certainty of a sample not having a variant at certain position depends on the number of reads covering that position: if there are no reads covering the position, we have no certainty at all; if there are many reads, we can be certain that the sample has REF allele at that position.

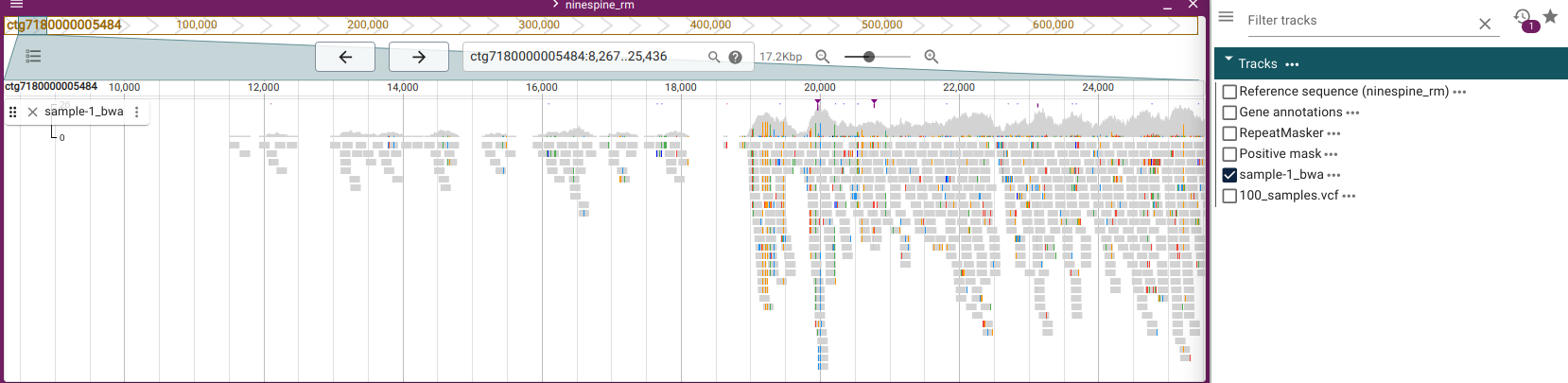
Using JBrowse2 genome browser and selecting “sample-1_bwa.bam”, we can indeed see that no reads are mapped before position 11,503 in that contig and up to around position 19,000, the mapping is very sparse:

Joint-call

The last part of the variant calling is this:

flowchart LR
    subgraph sample_1
    style sample_1 fill:#fdf2e9
    gvcf_1["&emsp13;gvcf_1&ensp;"]
    end
    subgraph sample_2
    style sample_2 fill:#fdf2e9
    gvcf_2["&emsp13;gvcf_2&ensp;"]
    end
    subgraph sample_n
    style sample_n fill:#fdf2e9
    gvcf_n["&emsp13;gvcf_n&ensp;"]
    end
    subgraph sample_100
    style sample_100 fill:#fdf2e9
    gvcf_100
    end

    gvcf_1 --> gvcf
    gvcf_2 --> gvcf
    gvcf_n --> gvcf
    gvcf_100 --> gvcf

    subgraph all_samples
    style all_samples fill:#fdf2e9
    gvcf --> vcf
    end

The individual GVCF files are merged into one file that contains a) information about variants in different samples, and b) information of non-variants in different samples. From that, a VCF file is created with information of all variants observed in different samples and each samples’ genotype at those variant positions. Crucially, the genotype information can be missing if the sample contains no data for that position.

In addition to that, the joint-call of many samples has the advantage that information from other samples helps to confirm a weak signal of a variant in the focal sample. For example, we could have coverage of five at a specific position and observe four times “A” and one time “G”. Without other information, it would be easy to conclude that “G” might be a base calling error (which happens with DNA sequencing devices). However, if other samples have shown that the position has the “G” variant, the single observation of “G” in the focal sample makes the heterozygous genotype “0/1” more plausible. We look at the maths behind genotype calling later.

Genotype likelihood

In the end, VCF files are huge tables where the rows are positions in the genome and (most of) the columns are genotypes of the samples at those positions. There is additional information to describe the genome position, and the columns for samples report more than the genotype.

Let’s assume a position in the genome of “sample_X”. Its BAM file looks like this:

The position 32417 is variable and is reported in the VCF file as:

#CHROM POS    REF   ALT                  FORMAT              SAMPLE_X
LG1    32417  A     T   <stuff removed>  GT:AD:DP:GQ:PL      0/1:1,3:4:25:110,0,25

The first four columns are quite obvious. After some missing columns, we have “FORMAT” and the sample, here called “SAMPLE_X”. The FORMAT field explains what is reported in the sample field. According to the header description, these are:

GT “Genotype”
AD “Allelic depths for the ref and alt alleles in the order listed”
DP “Approximate read depth (reads with MQ=255 or with bad mates are filtered)”
GQ “Genotype Quality”
PL “Normalized, Phred-scaled likelihoods for genotypes as defined in the VCF specification”

The first three should again be obvious. We have four observations at the position (DP=4) and these contain 1 A and 3 Ts (AD=1,3). From these, a heterozygous genotype (GT=0/1) seems reasonable.

GQ and PL describe the confidence on the chosen genotype and the two alternatives for that.

Given four nucleotides, there are ten possible genotypes:

AA	AC	AG	AT
	CC	CG	CT
		GG	GT
			TT

Although only two nucleotides are observed here (A and T), one could compute the likelihood for each of these giving the observed reads. Furthermore, the likelihood for none of the genotypes would be zero as the calculation considers the possibility of base calling errors.

Here, we know the two alleles and only the three possible genotypes produced by those (AA, AT, TT) are considered.

One approach for computing the genotype likelihood is:

\[ P(X|G=bh) = \prod_{i=1}^{r} (\frac{L_b^{(i)}}{2}+\frac{L_h^{(i)}}{2}) ~~~~ b,h \in {A, C, G, T} \]

We can break this into bits:

\(P(X|G=bh)\) means ‘likelihood of data (X) given that genotype (G) is “bh” where “b” and “h” are one of nucleotides’
\(\prod_{i=1}^{r}\) means ‘multiply over observed bases in “r” reads’
\(L_h^{(i)}\) means ‘likelihood of allele “h” producing base observed in read “i”’. This is divided by “2” as there is 50% chance of base coming from either allele
\(b,h \in {A, C, G, T}\) means ‘“b” and “h” are one of nucleotides A, C, G, T’

“bh” is one of the ten genotypes and we iterate through every genotypic configuration.

In the figure above, the first read had “A” at position 32417. The likelihood of observing that if the true genotype would be “AC” is computed as:

\[ P(X=A|G=AC) = \frac{L_A^{(1)}}{2}+\frac{L_C^{(1)}}{2} = \frac{1-\varepsilon}{2}+\frac{\varepsilon}{6} \]

where \(\varepsilon\) is the probability of an erroneous base call. Thus, the probability of observing “A” if the first allele is “A” is \(1-\varepsilon\), i.e. the probability of not calling “A” wrongly. On the other hand, the probability of observing “A” if the second allele is “C” is \(\varepsilon/3\), i.e. the probability of calling “C” wrongly; If the error rate is \(\varepsilon\), the probability of this erroneous call being “A” (and not “G” or “T”) is one third.

We can similarly calculate the likelihoods for all four reads:

\[ P(X=[A,T,T,T]|G=AC) = \]

\[ (\frac{L_A^{(1)}}{2}+\frac{L_C^{(1)}}{2}) (\frac{L_A^{(2)}}{2}+\frac{L_C^{(2)}}{2}) (\frac{L_A^{(3)}}{2}+\frac{L_C^{(3)}}{2}) (\frac{L_A^{(4)}}{2}+\frac{L_C^{(4)}}{2}) = \] \[ (\frac{1-\varepsilon}{2}+\frac{\varepsilon}{6})(\frac{\varepsilon}{3})(\frac{\varepsilon}{3})(\frac{\varepsilon}{3}) \]

We can can compute that with R:

e <- 0.00055
l <- ((1-e)/2+e/6)*e/3*e/3*e/3
round(log10(l),2)

[1] -11.51

The error rates used

Above, I’ve used the base calling error rate of 0.00055. In the sampling example below, the rate is 0.01. I’m not sure which rate the genotype calling functions use but the rate 0.00055 gave numbers that closely match the observed data. In reality, the genotype calling functions are probably more complex than this. The logic is similar nevertheless.

We can similarly compute the likelihood of the observed data (A, T, T, T) for each genotype:

Genotype	Likelihood(log10)
AA	-11.21
AC	-11.51
AG	-11.51
AT	-1.20
CC	-14.95
CG	-14.95
CT	-4.64
GG	-14.95
GT	-4.64
TT	-3.74

The three genotypes possible for the alleles A and T are in bold. Of these, “-1.20” for the heterozygote is the greatest and thus “0/1” is chosen as the most likely genotype. As was mentioned earlier, FASTQ, BAM and VCF data use Phred scores, i.e. \(-10~log_{10}(P)\).

Genotype	Likelihood(log10)	Phred-score
AA	-11.21	112.1
AT	-1.20	12.0
TT	-3.74	37.4

We had these for this site:

FORMAT              SAMPLE_X
GT:AD:DP:GQ:PL      0/1:1,3:4:25:110,0,25

Here,

PL is the difference between the best and this genotype
112.1 - 12.0 = 100
12.0 - 12.0 = 0
37.4 - 12.0 = 25
GQ is the difference between the best and the second best genotype
37.4 - 12.0 = 25

Uncertainty of small samples

We had only three reads for that variant position and observed one A and three T’s. If the number of A and T reads is the same, picking four reads randomly and observing one A and three T’s has the probability of 25%. With the same probability we would get three A’s and one T, and with the probability of 37.5% we would observe two A’s and two T’s. Those don’t make 100%.

Assume three boxes full of red and blue, red or blue balls:

Eyes blinded, we pick four balls from one of the boxes. Seeing the balls, can we know which box we picked them from?

Let’s assume that we have drawn four red balls: \(\color{red}\bullet \bullet \bullet\; \bullet\)

The probabilities for the data given the three boxes are:

\(P=0.5^4=0.0625~~~~\) \(~~~P=1~~~~~\) \(~~~P=0\)

However, in DNA sequencing data we have errors. Assuming that the error rate of 0.01, we have:

Then the probabilities for getting four red balls from the three boxes are:

\(P=(0.495+0.005/3)^4=0.061~\) \(P=(1-0.01)^4=0.961~\) \(P=(0.01/3)^4=1.23 \cdot 10^{-10}\)

The probability of drawing four red balls from the box containing blue balls is negligible; however, drawing four red balls from the box containing red and blue balls is over 6%, meaning that we are expected to get that when repeating the draw 17 times.

In DNA analysis, it means that heterozygotes can be missed when there are only a few reads covering the position. Having a heterozygote position “0/1” and four reads, we are expected to infer the genotype wrongly as “0/0” or “1/1” in 12.5% of the cases. That’s lot when we have potentially millions of variant positions.

Fortunately, the problem is not as great in all population genetic analyses. If we have many heterozygous samples, we are expected to the genotype right in 87.5% of the cases. In the remaining cases, the genotype is wrongly inferred but the error should be random and lead to “0/0” and “1/1” genotypes with equal probabilities. If that is the case, the allele frequency for that position is unaffected.

Likelihoods of homozygote and heterozygote genotypes

In the example of position “LG1:32417” above, the Genotype Quality, GQ, was 25 in the Phred scale, which is pretty good. (Remember that the Phred score “20” means that the chance of error is 1/100 or 1%; “25” means that the chance is 0.3%.) It would seem intuitive to use GQ as a filtering criteria and only consider genotypes above a certain threshold. With low coverage data, this has a serious drawback, however.

Let’s assume that the sequencing coverage at the position would be the same four but we would now observe four times T. Then, the likelihoods of the alternative genotypes are given as:

\[ P(X=[T,T,T,T]|G=AA) = (\frac{\varepsilon}{3})^4 \]

\[ P(X=[T,T,T,T]|G=AT) = (\frac{1-\varepsilon}{2}+\frac{\varepsilon}{6})^4 \]

\[ P(X=[T,T,T,T]|G=TT) = (1-\varepsilon)^4 \]

resulting to this table:

Genotype	Likelihood(log10)	Phred-score
AA	-14.95	149.5
AT	-1.20	12.0
TT	-0.00	0.01

Then, we can similarly compute the PL and GQ fields for the VCF file:

PL is the difference between the best and this genotype
149.5 - 0.01 = 149
12.0 - 0.01 = 12
0.01 - 0.01 = 0
GQ is the difference between the best and the second best genotype
12 - 0 = 12

This shows that with

observation [A,T,T,T], the best genotype is “0/1” and GQ is 25
observation [T,T,T,T], the best genotype is “1/1” and GQ is 12

Thus, if we use GQ for filtering, there is a great risk of removing homozygotes and keeping heterozygotes. Although the maths behind this are correct, this may not be what we want and such filtering may seriously bias the data.

On the population level, it is often better to accept that the genotypes inferred from low coverage data may be erroneous but trust that this error is random, giving approximately correct allele frequencies. If the question is “Can I trust the genotype call on this individual at that position?”, the GQ field is useful and tells the confidence on that particular call.

Take-home message

The genotype of a sample at a specific genome position is computed from the observed bases in short-reads spanning that position. The genotype quality and likelihoods are given using Phred scores. With low-coverage data, the likelihoods of alternative genotypes may be fairly similar and a wrong genotype may be “called”. Observing even a single alternative base makes the heterozygous genotype much more likely whereas observing multiple same bases doesn’t necessarily make the homozygous genotype equally clearly superior.

To save space, variant analyses are based on VCF-formatted data that only report the differences of specific samples from the reference individual. This way, the size of the data decreases from billions or hundreds of millions of sites to tens or hundreds of thousands of sites. When calling variants in multiple samples, it is important to distinguish positions that do not contain a variant from positions do not contain information. The GATK approach includes that information in the GVCF data; multiple GVCF files are then join-called to create a VCF file with variant information only.